Apr
24
การเคลื่อนที่แบบวงกลม
Circular Motion

ก่อนที่จะเรียนเรื่องการ เคลื่อนที่แบบวงกลม จะอธิบายปริมาณที่เกี่ยวข้องให้ผู้เรียนได้ทำความเข้าใจก่อน ซึ่งปริมาณที่เกี่ยวข้องประกอบด้วย คาบเวลา , ความถี่ , ความเร็วเชิงเส้น , ความเร็วเชิงมุม , ความสัมพันธ์ระหว่างความถี่กับคาบเวลา, ความสัมพันธ์ระหว่างความเร็วเชิงเส้นกับความเร็วเชิงมุม, ความเร่งสู่ศูนย์กลาง, แรงสู่ศูนย์กลาง, หลังจากนั้นผู้เรียนจะได้ศึกษาเกี่ยวกับลักษณะของการเคลื่อนที่แบบวงกลม เช่น การเคลื่อนที่เป็นวงกลมในแนวดิ่ง, การเคลื่อนที่เป็นวงกลมในแนวราบ, การเคลื่อนที่เป็นวงกลมแบบกรวยกลม, การเลี้ยวโค้ง, การเคลื่อนที่ของดาวเคราะห์และ การเคลื่อนที่ของประจุไฟฟ้าในสนามแม่เหล็ก (ภาพตัวอย่างการเคลื่อนที่แบบวงกลม)
………………………………………
คาบ เวลา และความถี่
(period & frequency)
…………………………………………ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แบบวงกลมด้วยอัตราเร็วคงที่
1.คาบ (Period) "T" คือ เวลาที่วัตถุเคลื่อนที่ครบ 1 รอบ หน่วยเป็นวินาที่/รอบ หรือวินาที
2.ความถี่ (Frequency) "f" คือ จำนวนรอบที่วัตถุเคลื่อนที่ได้ภายในเวลา 1 วินาที หน่วยเป็นรอบ/วินาที หรือ เฮิรตซ์ (Hz)
ที่ โดยคาบและความถี่สัมพันธ์กันโดย
………………………………………
ความสัมพันธ์ระหว่างอัตราเร็ว คาบเวลา และความถี่
………………………………………
(T=1/f)
………………………………………
ความเร็วเชิง เส้น และความเร็วเชิงมุม
(linear velocity & angular velocity)
………………………………………
………………………………………
ความ สัมพันธ์ของความเร็วเชิงเส้นและความเร็วเชิงมุม
( Relationship between linear velocity & angular velocity )
………………………………………แต่ในที่นี้ยังมีอัตราเร็วอีกประเภทหนึ่ง ซึ่งเป็นการบอกอัตราการเปลี่ยนแปลงของมุมที่จุดศูนย์กลาง เนื่องจากการกวาดไปของรัศมี ใน 1 วินาที เรียกว่า อัตราเร็วเชิงมุม (w) อ่านว่า โอเมก้า
นิยามอัตราเชิงมุม (w) คือ มุมที่รัศมีกวาดไปได้ใน 1 วินาทีมีหน่วยเป็น เรเดียน/วินาที
การบอกมุมนอกจากจะมีหน่วยเป็นองศาแล้ว ยังอาจใช้หน่วยเป็นเรเดียน (radian) โดยมีนิยามว่า มุม 1 เรเดียน มีค่าเท่ากับมุมที่จุดศุนย์กลางของวงกลม ซึ่งมีเส้นโค้งรองรับมุมยาวเท่ากับรัศมี หรือกล่าวได้ว่ามุมในหน่วยเรเดียน คือ อัตราส่วนระหว่างส่วนเส้นโค้งที่รองรับมุมกับรัศมีของวงกลม
ถ้า a คือ ความยาวองส่วนโค้งที่รองรับมุม
r คือ รัศมีของส่วนโค้ง
q คือ มุมที่จุดศูนย์กลางเป็นเรเดียน
ความสัมพันธ์ระหว่างมุมในหน่วยองศากับเรเดียน
เมื่อพิจารณาวงกลม พบว่ามุมรอบจุดศูนย์กลางของวงกลมเท่ากับ 360 องศา โดยส่วนโค้งที่รองรับมุมก็คือเส้นรอบวงนั้นเอง
ดังนั้น สรุปได้ว่า มุม 360 องศา เทียบเท่ากับมุม 2p เรเดียน
เมื่อพิจารณาวัตถุเคลื่อนที่แบบวงกลมด้วยอัตราเร็วคงที่ครบ 1 รอบพอดี
ซึ่งเป็นความสัมพันธ์ระหว่างอัตราเร็วเชิงเส้น (v) และอัตราเร็วเชิงมุม (w)
………………………………………
ความเร่งสู่ศูนย์กลาง
(Centripetal acceleration)
………………………………………
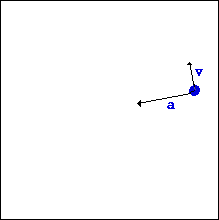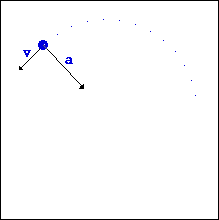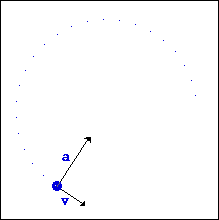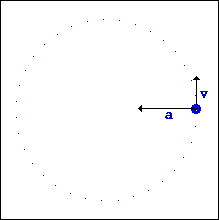
- ถ้าวัตถุเคลื่อนที่ด้วยอัตรา เร็วคงที่ เช่นวงกลมในแนวราบ จะเกิดความเร่งเข้าสู่ศูนย์กลางเพียงแนวเดียว 





………………………………………
แรงสู่ศูนย์กลาง
( Centripetal Force )
………………………………………
………………………………………
การเคลื่อนที่เป็นวง กลมในแนวราบ
(Virtical curve motion)
………………………………………
วัตถุจะไม่เปลี่ยนระดับในการเคลื่อนที่ แรงเข้าสู่ศูนย์กลางจะเท่ากันทุกตำแหน่ง
………………………………………
การ เคลื่อนที่เป็นวลกลมในเเนวดิ่ง
Conical Pendulum
………………………………………
วัตถุจะเปลี่ยนระดับในการ เคลื่อนที่ ดังนั้นแรงเข้าสู่ศูนย์กลางในแต่ละตำแหน่งจึงไม่เท่ากัน
พิจารณาลูกกลมโลหะ ซึ่งเคลื่อนที่ตามรางเรียบรูปวงกลมในแนวดิ่ง โดยเคลื่อนที่รอบด้านในของวงกลม เส้นทางการเคลื่อนที่ของลูกกลมโลหะจะเป็นแนววงกลมในระนาบดิ่ง ทุก ๆ ตำแหน่งที่ลูกกลมโลหะจะต้องมีแรงสู่ศูนย์กลาง เพื่อเปลี่ยนทิศทางความเร็วของลูกกลมโลหะ ให้เคลื่อนที่เป็นวงกลม แรงสู่ศูนย์กลางนี้เกิดจากรางออกแรงดันลูกกลมโลหะ ซึ่งเป็นแรงปฏิกิริยาของรางที่โต้ตอบกับแรงที่ลูกกลมโลหะออกแรงดันราง และแรงสู่ศูนย์กลางบางช่วงจะมาจากแรงโน้มถ่วงที่กระทำต่อลูกกลมโลหะ ในกรณีลูกกลมโลหะมวล m อยู่ ณ ตำแหน่งล่างสุดของรางที่มีรัศมีความโค้ง r ให้แรงที่รางดันลูกกลมโลหะในแนวตั้งฉากกับผิวของรางเท่ากับ F และแรงที่โลกดึงดูดลูกกลม คือ mg แรงลัพธ์ของแรงทั้งสองคือ แรงสู่ศูนย์กลาง
~ ถ้าลูกกลมอยู่ ณ ตำแหน่งสูงสุด จะได้
การเคลื่อนที่แบบกรวยกลม
Conical Pendulum
เชือกเบายาว L ปลายข้างหนึ่งติดวัตถุมวล m อีกปลายตรึงแน่นแกว่งให้วัตถุเคลื่อนที่เป็นวงกลมในแนวราบ รัศมี r ด้วยอัตราเร็วคงที่ v และเชื่อกทำมุม q กับแนวระดับดังรูป
ขณะมวล m เคลื่อนที่เป็นวงกลมในแนวราบ ได้รับแรงกระทำ 2 แรงคือ แรงตึงเชือกและน้ำหนังของวัตถุ
เมื่อแตกแรงต่าง ๆ แล้วจะได้
เมื่อพิจารณาในเเนวดิ่ง
 เมื่อพิจารณาในเเนวราบ วัตถุเคลื่อนที่เป็นวงกลม
เมื่อพิจารณาในเเนวราบ วัตถุเคลื่อนที่เป็นวงกลม
หรือเราอาจนำสมการทั้ง2สมการมาสัมพันธ์กันได้

………………………………………
การ เคลื่อนที่บนทางโค้ง
Curve Motion
………………………………………
………………………………………
การหา มุมเอียงของรถจักรยานยนต์ขณะเลี้ยว
………………………………………
ขณะเลี้ยวรถแรงกระทำต่อรถมี mg, N และ f ซึ่งแรง N และ f รวมกันได้ เป็นแรงลัพธ์ R C.M. จะก่อให้เกิดโมเมนต์ ทำให้รถคว่ำขณะเลี้ยวดังรูป ถ้าไม่ต้องการให้รถคว่ำต้องเอียงรถ ให้จุดศูนย์กลางของมวล ผ่านแนวแรง R ขณะเลี้ยว รถจึงเลี้ยวได้โดยปลอดภัยไม่พลิกคว่ำดังรูป รูปแสดงแรงกระทำต่อรถจักรยานยนต์ขณะเลี้ยวบนถนนโค้งราบ
ถ้าเลี้ยวรถรถด้วยอัตราเร็วสูงสุด พบว่า
ไม่ว่ารถจักรยานยนต์เลี้ยวโค้งแล้วเอียงรถ หรือ รถจักรยานยนต ์เลี้ยว โค้งบนพื้นเอียงลื่น มุม q ที่เกิดจากการเอียงของทั้งสองกรณีคือมุมเดียวกัน ใช้สูตรเดียวกันคือ
………………………………………
การเคลื่อนที่เป็น วงกลมของดวงดาว
………………………………………
ที่มา
Subscribe to:
Post Comments (Atom)











Post a Comment